树

树的定义

完全二叉树

树的遍历

前缀树Trie

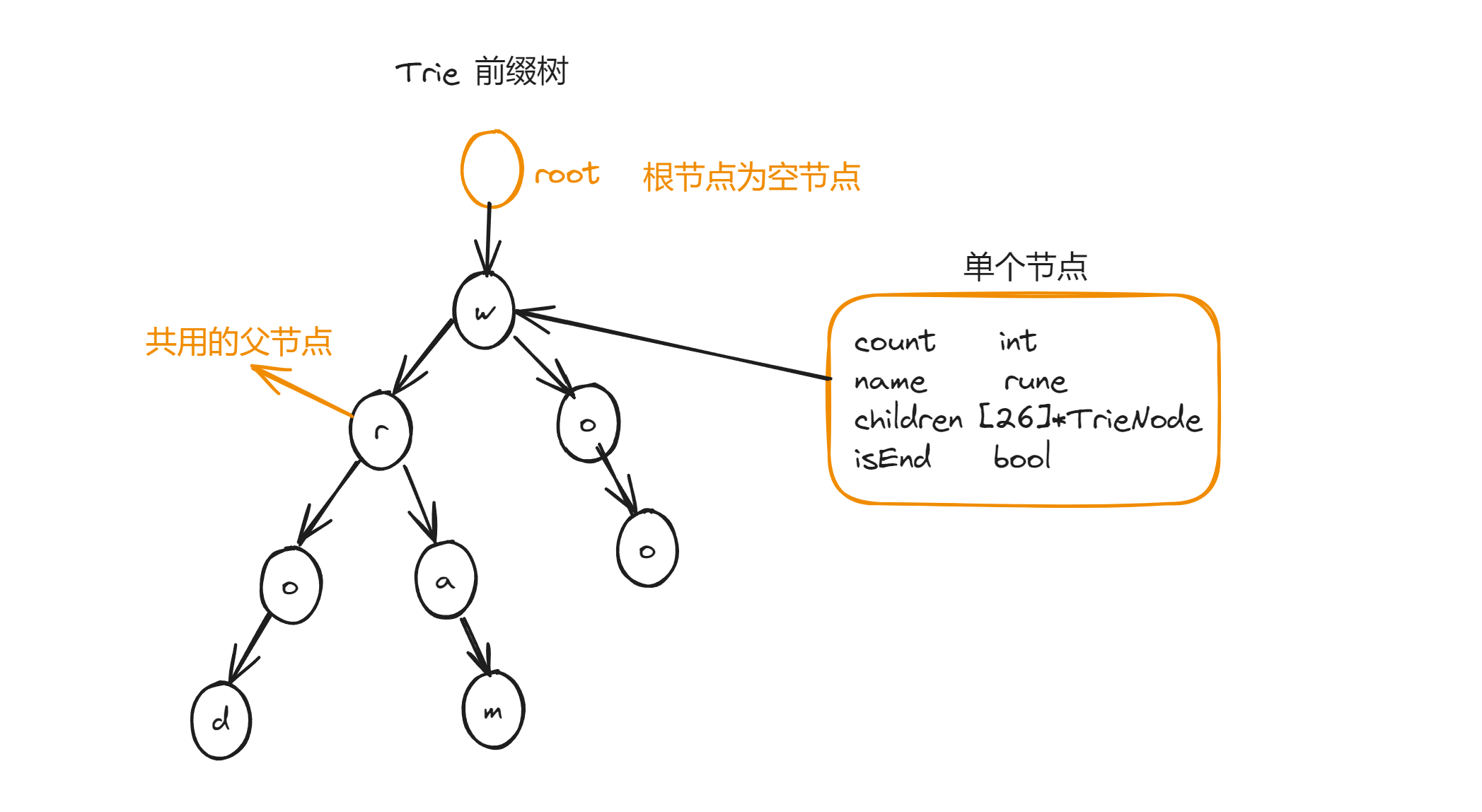
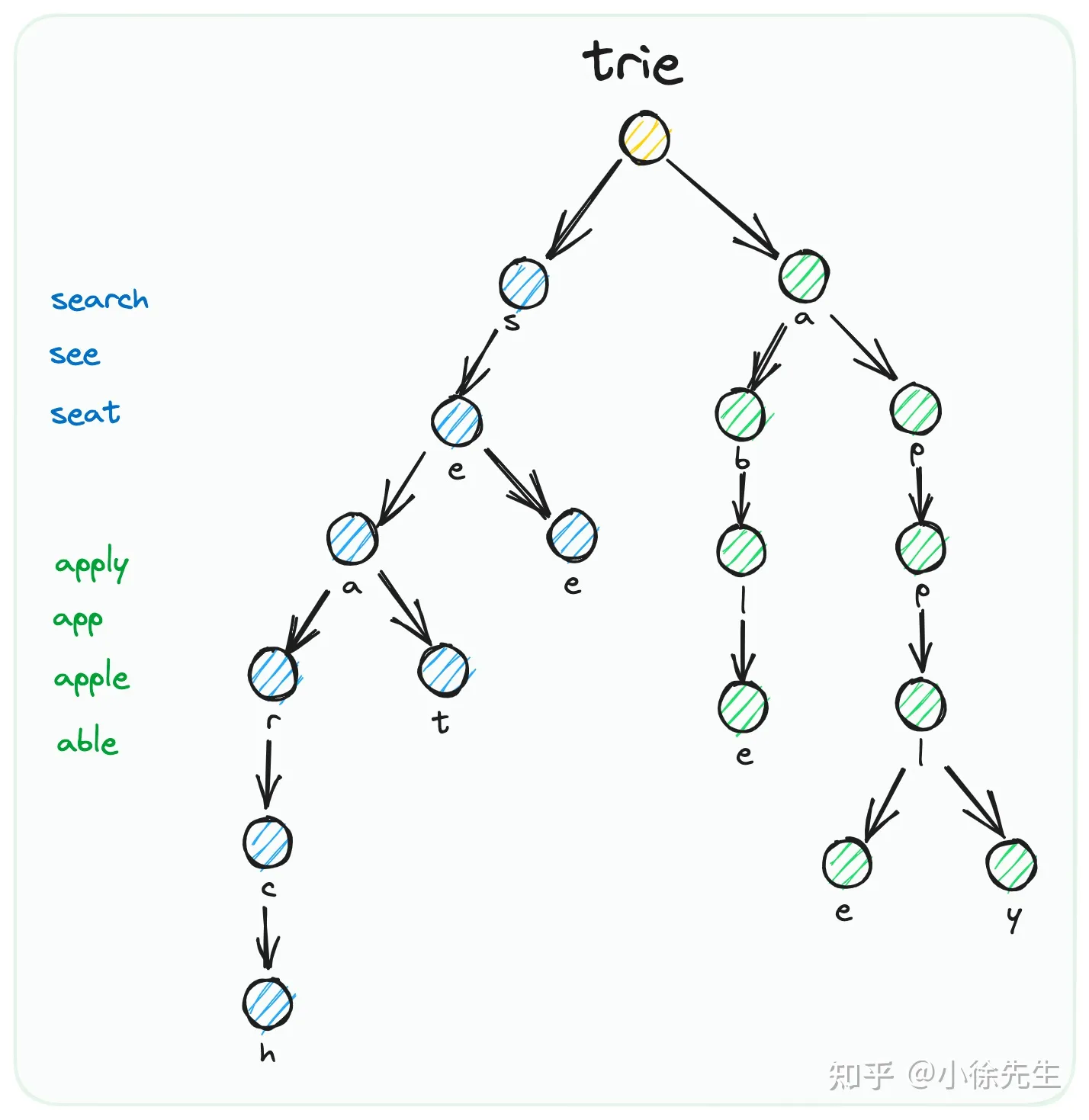
Alt text

前缀树trie又称为字典树或者单词查找树，是一种广泛应用于文本查找，路由查找的存储数据结构。

trie是一个多叉树结构，树中的每个节点存储一个字符，它与普通树状数据结构最大的差异是，存储数据的key不存放在单个节点中，而是从根节点root出发一直到目标节点target node 之间的沿途路径组成。这样的构造方式最大的好处是，拥有前缀相同的字符串可以复用公共的父节点，直到在首次出现不同字符的位置才出现分叉，形成多叉树结构。 leetcode习题

初始化节点

type Trie struct {
	root *TrieNode //根节点
}

type TrieNode struct {
	count    int //经过该节点单词的数量
	name     rune //用来存储单词，可不加
	children [26]*TrieNode //子节点，定义为26个字母
	isEnd    bool //是否为尾节点
}

插入

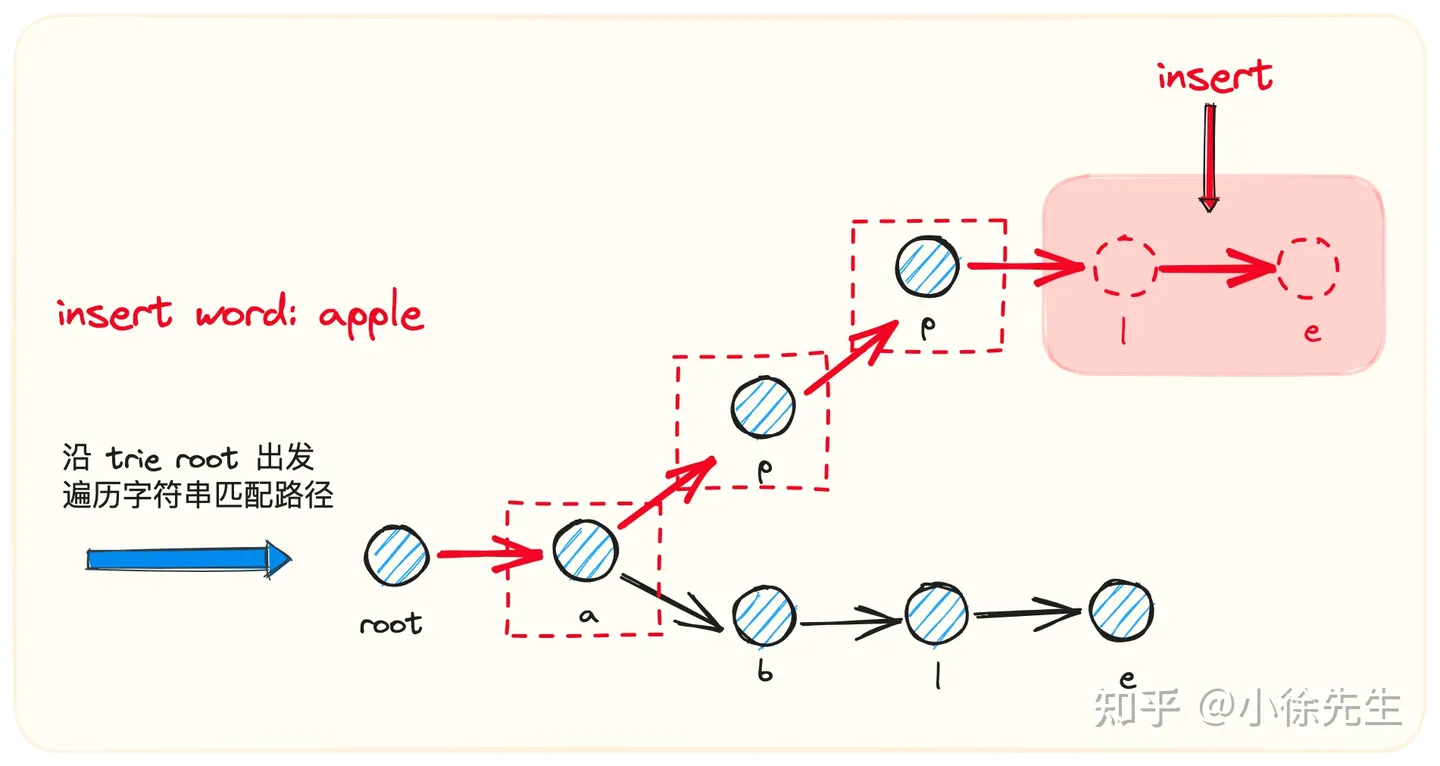
Alt text

    // 插入
func (t *Trie) insert(word string) {
    //node指向根节点
	node := t.root
    //遍历单词的每个字母
	for _, v := range word { 
		if node.children[v-'a'] == nil { //确定一个字母在子节点数组中的位置 [字母-'a']。
        
            //等于nil说明树中不存在这个字母,创建一个新的节点存储
			node.children[v-'a'] = &TrieNode{
				name:     v,
				children: [26]*TrieNode{},
				isEnd:    false,
			}
		}
		node = node.children[v-'a'] //存在就直接取出,node指向下一个节点
		node.count++//统计经过字母的单词数量
		fmt.Println(node.name, "-", node.count)
	}
	node.isEnd = true //单词结尾

}

查找

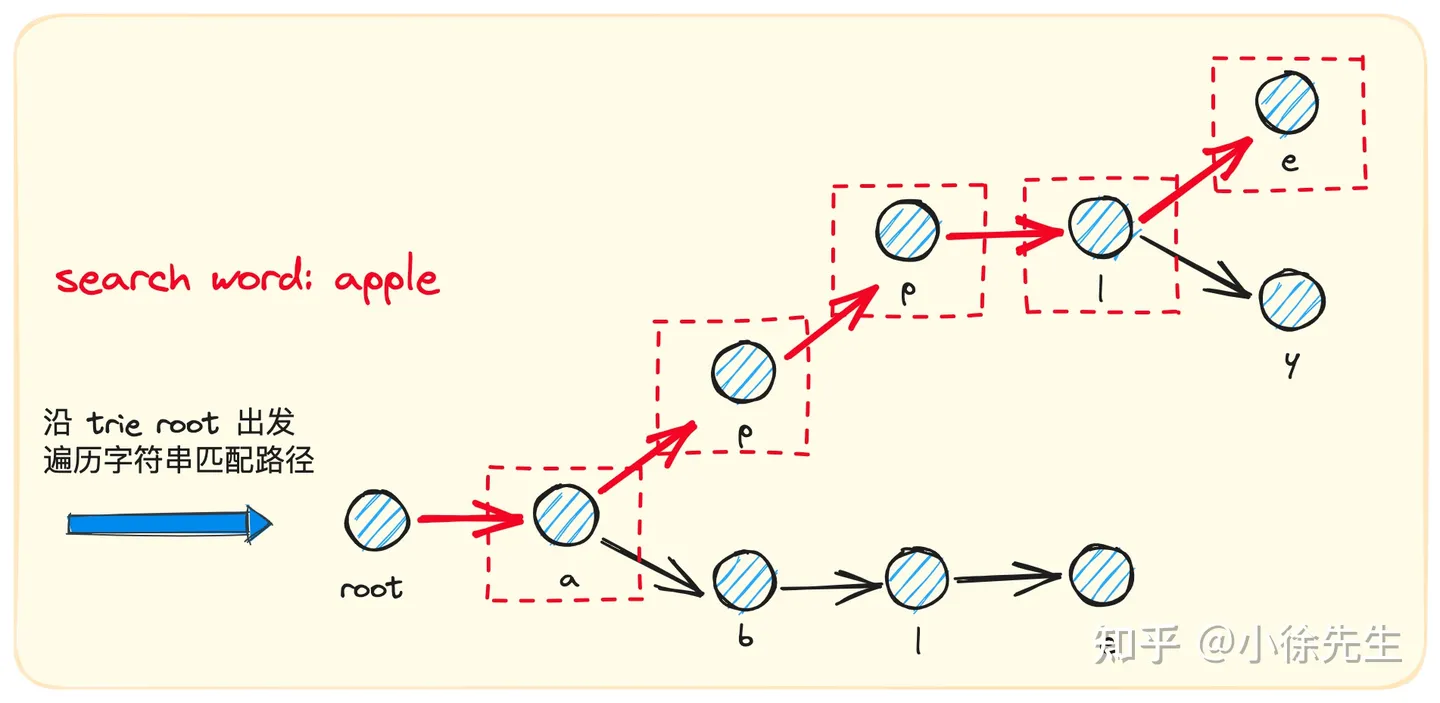
Alt text

// 搜索单词
func (t *Trie) search(word string) bool {
	node := t.root
	builder := strings.Builder{}//存储读取到的字母
	for _, v := range word {
		if node.children[v-'a'] == nil { //树中不存在这个字母直接返回false,说明没存储这个单词
			return false
		}
		builder.WriteRune(node.children[v-'a'].name)
		node = node.children[v-'a']//移动到下一个节点
	}
	fmt.Println(builder.String())
	return node.isEnd//单词最后一个节点isEnd必定为true
}

// 查找是否以某个前缀开头,代码与search查不到,差异是不用判断是否到单词尾结点了
func (t *Trie) StartWith(prefix string) bool {
	node := t.root
	for _, v := range prefix {
		if node.children[v-'a'] == nil { //树中不存在这个字母
			return false
		}
		node = node.children[v-'a']
	}
	return true
}

统计

// 统计应用该前缀的单词数量
func (t *Trie) CountPrefix(prefix string) int {
	node := t.root
	for _, v := range prefix {
		if node.children[v-'a'] == nil {
			return -1
		}
		node = node.children[v-'a']
		fmt.Printf("count_prefix:%c-%d\n", node.name, node.count)

	}
	fmt.Printf("count_prefix最后一个字母:%c\n", node.name)
	return node.count //返回前缀最后一个字母节点的count
}

压缩前缀树

gin的路由存储使用了压缩前缀树。